Contents
はじめに
IDL の overplot の使い方は以下の通りで、plot() に /overplot キーワードを追加するだけです。
plt = plot(x, y, /buffer)
plt = plot(x, y, /buffer, /overplot)ちなみに /buffer はプロットした図を画面に表示させないということを意味しています。
プロットした図をその場で確認したい方は、 /buffer を削除してください。
overplot の具体例
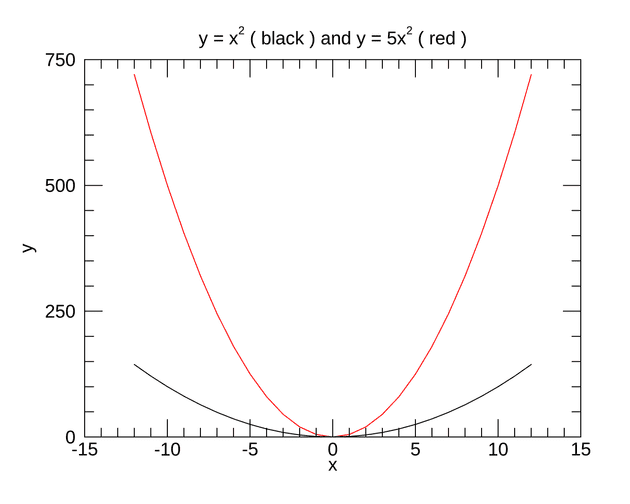
例として y = x^{2} と y = 5x^{2} を -12 <= x <= 12 の範囲で重ね書きしてみます。
以下のプログラムを拡張子 .pro のファイルとして IDL のパスが通っているフォルダに保存してください。
pro sample_overplot
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
; x [-12, 12] の範囲で
; y1 = x^2 と y2 = 5x^2 を重ね書きする
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
saveDirName = '~/Downloads/'
saveFileName = 'figure_sample_overplot.png'
x = dindgen(25, start = -12, increment = 1)
y1 = x^(2d)
y2 = 5 * x^(2d)
plt = plot(x, y1,$
; x
xtitle = 'x',$
xrange = [-15, 15],$
xtickvalues = [-15, -10, -5, 0, 5, 10, 15],$
xtickname = xtickvalues,$
xminor = 4,$
; y
ytitle = 'y',$
yrange = [0, 750],$
ytickvalues = [0, 250, 500, 750],$
ytickname = ytickvalues,$
yminor = 4,$
; title
title = '$y = x^{2}$ ( black ) and $y = 5x^{2}$ ( red )',$
; linestyle
linestyle = 0,$ ; solid line
thick = 1,$
color = 'black',$
; symbol
symbol = 'o',$
sym_size = 0,$
sym_color = 'black',$
sym_filled = 1,$
; font
font_size = 14,$
font_name = 'Helvetica',$
; option
/buffer)
plt = plot(x, y2,$
; linestyle
linestyle = 0,$ ; solid line
thick = 1,$
color = 'red',$
; option
/buffer,$
/overplot)
plt.save, saveDirName + saveFileName
enddindgen(配列の要素数, start = 配列の初期値, increment = 配列の間隔)で double 型の配列を作成しています。例えば、要素数10個の奇数配列を作成したければ、oddArray = dindgen(10, start = 1, increment = 2)とすれば良いです。
plt.save, saveName でプロットした図を保存しています。
今回は saveName を saveDirName + saveFileNameに分けて書いていますが、分けずに書いてもOKです。
個人的には分けて書くことをお勧めします。
複数の図を別名で同じディレクトリに保存する時に、ディレクトリとファイル名を分けて書いておいたほうが分かりやすいと思いますので。
このプログラムを実行すると、ダウンロードフォルダに以下に示すような figuresampleoverplot.png という画像ファイルが保存されます。
おわりに & 参考資料
この先には、左の軸と右の軸が異なる量をプロットする方法や、errorplot による誤差棒付きのプロット、などの応用編が待ち構えています。
応用編についても記事を書いていますので、公開するまで少々お待ちください。
idl の plot についての基本については、idl plot にまとめていますので、ご覧いただければ幸いです。
本記事は下記の資料を参考にして作成しました。
お勧め参考書は以下の書籍です。
最後までお読みいただき、ありがとうございました:)
愛用品
- Xiser Pro Trainer
1日中踏み続けられる強靭なステッパーでおすすめです. - HHKB Professional 墨
x HHKB キートップセット 白
ボディは墨色キートップは白色なのでめちゃめちゃ目に優しいのでおすすめです. - Apple Magic Mouse 2
トラックパッドは指が攣りそうになりますけどマウスはその心配が無いのでおすすめです. - Apple MacMini
ミニマルでパワフルなデスクトップ PC なので個人的に大好きなのでおすすめです. - iiyama Display 27inch FullHD
鮮明すぎない画面で目も疲れにくいですし何より高さ調節できるのが最高なのでおすすめです. - KINTO UNITEA 550ml
500ml の大容量でこの綺麗なデザインは他にみたことがないのでおすすめです.